草根影响力新视野　钟艺 编译

近日，一位业余的数学家解决了专业数学家从1950年开始就一直在研究的问题。

Aubrey de Grey是一名生物学家，他以试图彻底延长人类寿命而闻名，特别是他关于长寿的言论让全世界人民印象极为深刻——他宣称现在还活著的人将能享受到生物科技的慷慨馈赠，成为历史上第一波活到1000岁的人类。

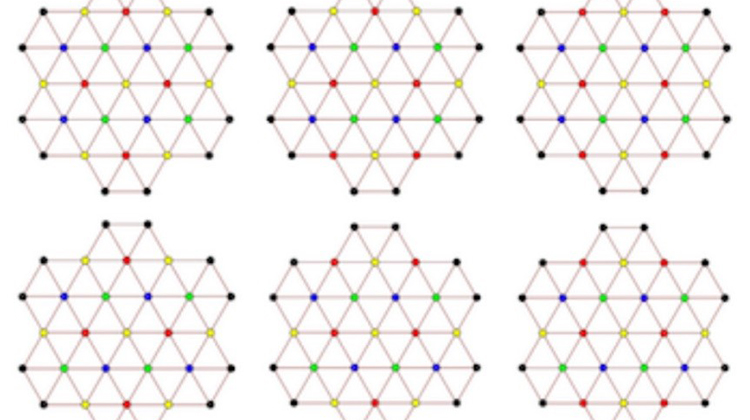
在今年四月份，Grey于科学预印本网站arxiv.org上发表了一篇论文，题目为《平面染色数最少是5》。在论文中Grey所讨论的是Hadwiger-Nelson问题，此问题属于欧式平面色数领域：如果给平面上所有的点都赋予一个颜色，那麽至少需要多少种颜色才能保证存在一种著色方法，使得任意两个距离为1的点是不同色？数学家经过几十年的研究，将最终的答案缩小范围在4,5,6,7之间。在之后的时间里，也陆陆续续有不少数学家对此问题进行深入研究，但数字上下范围都没有新版本出现。

从Grey的职业来说，他距离解答出难度系数如此之高的数学问题其实有很大的距离，但Grey却喜欢在闲暇之余以数学问题和棋牌游戏进行放松。在一次棋牌比赛里，他与一群也热衷于黑白棋的数学家同场竞技，他们向Grey介绍了数学界著名的图论，从此这些和数学紧密相关的颜色问题就在他心里扎下了根。

Grey在一次闲来无事的Hadwiger-Nelson问题研究中发现，数学家数十年来所做的假设实际上是有问题的。在刊发的论文中，Grey表明：一个包含1581个点的平面图至少需要5种不同的颜色来著色才能保证每两个点的颜色是不重复的。Grey的论点对于数学领域来说是一个进展，60多年的僵局终于有人打破。

世界上有很多难题都是因为偶然的机会被攻破，就像当初业余数学家之王费马对微积分的重要贡献一样。当我们把这些看似偶然的跨界案例放在一起，其实能透过“偶然”看到“必然”的本质。

跨界成功的原因有一点很重要——灵感。灵感是“大脑自由”的一种体现，长时间用同一种思维方式进行研究和解决问题，脑子更容易陷入僵局，形成思维定式，反倒是那些没有被太多规矩捆绑的人会 “灵光乍现”，发现问题解决的契机。作为普通人，我们很难从这些大咖的成功案例里复制出知识和智商，但是我们也能从中悟出一些收获。

从孩子教育上来说，家长需要尊重和引导孩子思维形成的过程，不要盲目将自己认为对的方式强加到孩子身上，因为这会无形中给孩子的思维创建一座围墙，这座思维的墙一旦创建，后期很难再拆解掉。在最近很火的一档亲子类节目《超人妈妈》里，霍思燕的教育方式被很多网友点赞，她习惯于尊重孩子的想法和尝试，在孩子按照自己的方式碰壁之后，她是孩子寻求帮助的资源库，但不会手把手帮助或者替代孩子完成任务。

从个人成长来说，如果你有一个坚持了很长时间的兴趣那是很棒的事，不要随便把它丢弃。在匆忙的都市生活中，人们的生活已经趋于循规蹈矩，这时，你的兴趣就会像是一根救命稻草，把你从一成不变的反反复复中带离出来，帮助你找到“新鲜”和“活力”，赋予你“灵光乍现”机会。

 

Reference :

This Biologist Cracked a Problem That’s Stumped Mathematicians for 68 Years